Self-organizing multimodal codes

Learning Multimodal Representations

Multimodal foundation models (e.g. vision-language-action) are becoming increasingly important for AI applications spanning from multimedia document understanding to robotics. These models are capable of processing multiple modalities of data (e.g. images, text, audio) for reasoning and executing tasks. Research has shown that the power of these multimodal models rests largely in their ability to construct effective embeddings and embedding relationships between the different data types. We can think of embeddings like the "codes" in information theory parlance which are an alternative, often compressed, representation of the observed data that aims to preserve information. Now in the context of multimodal encoding, we aim to perserve information and additionally preserve relationships to other pieces of information.

Multimodal representations are pivotal for embodied AI systems. Here the RT-2 robot by Google DeepMind Research [1] uses a vision-language-action model to integrate natural language instruction with computer vision data to generate action plans. (Video Source: [1])

The design space for building multimodal models is large. For example, different data modalities can have shared or separate encoders, a variety of objective functions may be used, and training can be done with various weight initializaitons techniques. Biology hints that separate encoders for separate data modalities (e.g. audio, visual) is ideal, but how cognitive systems adaptively link these separate data encodings to each other remains a deep area of rearch both in neuroscience and AI. Temporal and spatial alignment/coherence have been evidenced to support early multisensory integration in brains [2]. However, the human brain operates in an dynamic online learning manner that naturally allows these coherences to be detected unlike AI models today which are more restricted to periodic training on batches of data. Thus alternative learning approaches have been explored to enable AI models to integrate data into meaningful representations. Contrastive learning is one such approach that has gained momentum and realized success in training large multimodal models today.

Contrastive Learning

Contrastive learning is a machine learning paradigm for learning data distributions by comparing individual data samples with each other. The goal is to have the model learn how to discern which data points are similar to each other and which are dissimilar. Contrastive learning achieves this by encoding data observations into a metric embedding space such that related encodings are pulled closer together (according to some distance metric) while unrelated data encodings are pushed futher apart. Defining how data observations are related to each other suggests some a-priori information or pre-made, supervised labeling. While supervised labeling could be used, contrastive learning is largely motivated to be used as a self-supervised method that doesn't rely on explicit labels. Thus, self-supervised contrastive learning leverages natural characteristics intrinsic to the data to develop the training signal to conduct the learning by comparison. For example, data similarity can correspond to data falling within certain time windows for sequential data, or soft classes can be defined over variations of a data sample that has been augmented through noise or spatial tranformations.

First introduced in [3], early self-supervised contrastive learning loss functions used one positive and one negative sample. The contrastive loss takes a pair of inputs $(x_i,x_j)$ and minimizes the embedding distance when they arise from the same class, otherwise it will maximize the distance. This contrastive loss objective can be expressed as the following:

Further extensions to contrastive learning have expanded the training objective to include multiple postive and negative pairs in the same batch. For instance, the triplet loss presented in FaceNet [4] learned distance measures between triplet sets of data samples with one anchor sample, one positive sample, and one negative sample. A critical and non-trivial factor for training with this objective is selecting challenging, useful negative samples for each triplet set.

Here $x$ , $x^{+}$ , and $x^{-}$ are anchor, postive, and negative samples respectively.

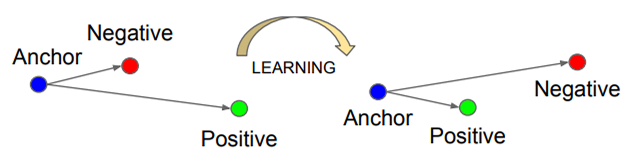Figure 2. Visualization of embedding transformations using a triplet loss objective. After learning, the model moves positive samples embeddings closer to the anchor embedding and negative samples further away. (Image Source: [3])

The lifted structure loss introduced by (Song et al, 2015) augments the triplet embedding to utilize all the pairwise edges for the data samples within a training batch [5]. They optimized the computational efficiency for this batched data sample comparison and incorpated importance sampling to bias the samples to include difficult negative sampels given a few random postive pairs instead of using uniform random sampling. The multi-class N-pair loss [6] also generalized the triplet loss to enable comparison with multiple negative data samples. If only one negative sample is compared per class, this loss converges to the softmax loss for multi-class classification.

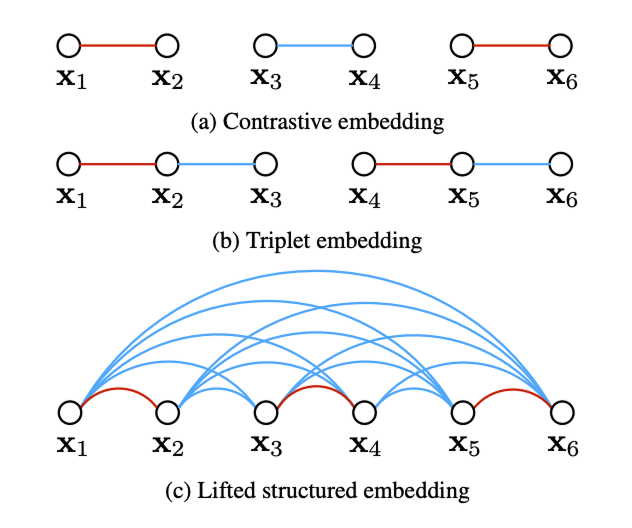Figure 3. Visual comparison of the the normal contrastive loss, the triplet loss, and the lifted structure loss. Red lines indicate similar pairing and blue lines represent dissimilar pairs. The lifted structure embedding takes into account all pair wise edges within the batch during learning. (Image Source: [4]) 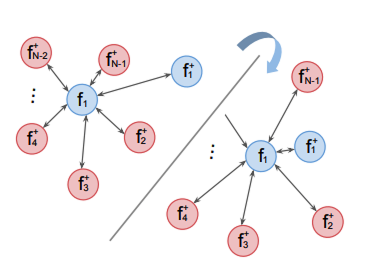Figure 5. Visualization of the N-Pair loss (Image Source: [6])

A connection can be made between information theory and contrastive learning which can be useful to apply this self-supervised approach to more general generative models of data. Contrastive predictive coding (CPC) with an information noise contrastive estimation loss (InfoNCE) [7] is foundational work in this domain that models the shared information between different parts of high-dimensional data. The CPC method combines predicting future obersvations with a probabilistic loss that aims to maximize mutual information between the predicted target and the given contextual data. The experimental setup for training these models is equivalent to in-painting tasks for images or fill-in-the-blank tasks for natural language. The model must autoregressively predict the unseen latent representations using a categorical regression function that discerns "real" data samples from "noise" or dissimilar data samples.

Multimodal Contrastive Learning

In the beginning, contrastive learning methods were applied to data of the same modality, but eventually research explored the self-supervised representation learning comparing data from different modalities. The CLIP embedding [3] was seminal work in for multimodal contrastive learning and leveraged the rich embeddings of natural language and images created by transformer models. In CLIP embedding models the dataset is composed of image-text pairs from captioned images. The images and text are then separately encoded into embedding vectors of equal dimension. The image embeddings can then act as a training signal or soft class label for the text embeddings, pulling other similar text embeddings closer and and dissimilar ones further away. The authors of CLIP trained on over 400M captioned images.

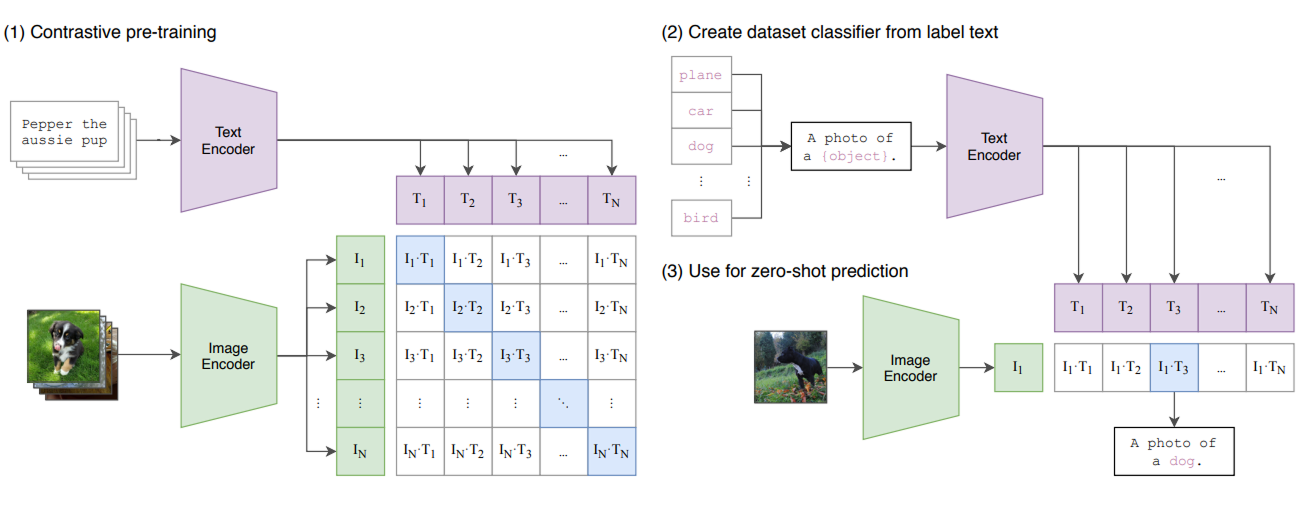
One of the main challenges with CLIP is its reliance on a large amount of highly curated data for training (e.g. 400M+ text-image pairs). There is a scarcity of multimodal data examples encompassing other data modalities beyond image-text in the real world, especially at the scale needed to train large transformer models. CLIP also struggles to capture fine-grained relationships between images and text and is limited to only mapping global image and text features. For example, models trained with CLIP perform poorly on tasks requiring object localization, object counting or spatial reasoning within images. Another significant challenge is that the algorithm requires every negative (dissimilar) pair to be compared for each data point to develop the embedding space. This process becomes exponentially expensive computationally as the dataset grows. Moving to an unsupervised regime would be ideal to preclude the need fo expensive and potentially biased external, manually designed labels. Moreover, pushing negative samples apart would ideally not require exhaustively comparing every pairwise combination of data samples.

Extending Contrastive Learning with Clustering

To circumvent the computational burdern of explicit pairwise feature comparison in contrastive methods, clustering can be used to group similar encodings in a memory and compute efficient way. Swapping Assignments between Views (SwaV) is a self-supervised contrastive learning approach that replaces the expensive pairwise data comparison with a clustering technique [9]. It utilizes a set of prototype vectors to represent anchors for the latent embedding code vectors.

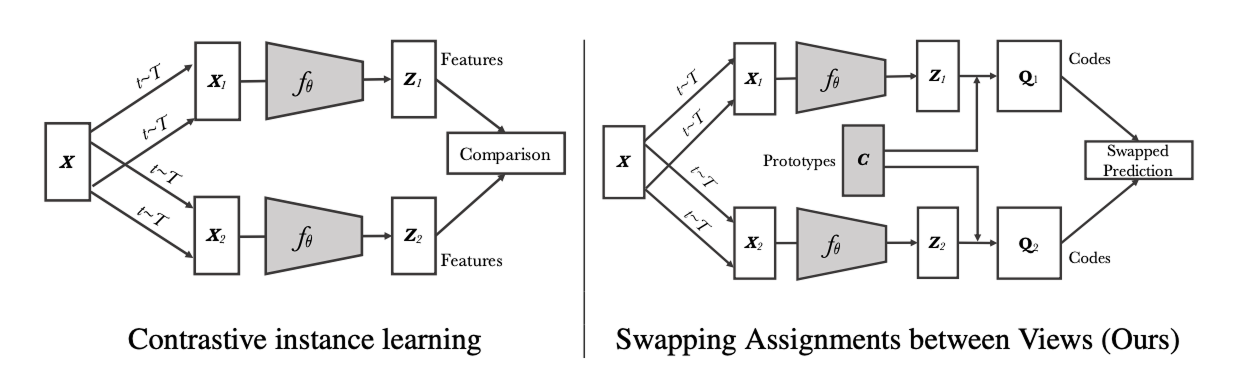
While SwaV was implemented on data from within the same modality (e.g. images with different views), [10] extended this idea to the cross-modal regime to make the SwaLIP model. SwaLIP is marries ideas from CLIP and SwaV, leveraging prototype code vectors and a clustering criteria to a CLIP objective.

Overall, evidence suggests that unsupervised, contrastive learning that also uses online, adaptive clustering would lead to powerful multimodal embeddings. How to achieve this is still an open area of research with a rapidly growing amount of proposed approaches. In the next section, I will introduce self-organizing methods as a direction that can potentially unlock the capacity to adaptively learn clusters within a contrastive learning of multimodal data representations.

Self-Organizing Intelligence

You may have heard of the famous 2000 neuroscience study from Eleanor Maguire that showed London taxi drivers who went through training developed enlarged hippocampi [11]. This result reveals the plasticity available in the memory center of the brain even into adult years. A finding from the same study that is less discussed however, is that the researchers found not only an enlargement of the posterior region of the hippocampus, but also a shrinkage in the anterior region of the same subjects. This finding suggests, that memory doesn't just grow with demand, but rather it shifts, or rearranges...it self-organizes.

Self-organization is a natural phenomenon where biological and physical systems express global order that organically emerges from internal, local processes. Examples of self-organizing behavior include geese flying in V formation, or naturally oscillating chemical reaction-diffusion processes, or even the arrangement of cortical folding in brains. Self-organizing systems do not require supervision, blue-prints, or pre-existing templates for pattern formation to occur. All of the global patterns in these systems arise soley from lower-level interactions utilizing local information.

A compelling characteristic of self-organizing systems is their ability to naturally represent complex data landcapes that may posses a myriad of clusters. This organic clustering is possisble because these systems typcially pass information laterally among other representational units, naturally forming conceptual neighoborhoods/topologies. The adaptive control of clustering data is in many ways a reflection of intelligence yet modern deep networks still lack this capability.

Figure 5. A python implementation of the Belousov-Zhabotinsky (B-Z)reaction-diffusion process. The B-Z process is an example of a self-organizing system that also naturallyexpresses different modes.

Self-Organizing Multimodal Embeddings

Today's state-of-the-art networks are large pretrained networks trained on large troves of data. While pretrained networks have made large strides for large language models recently, these models today still face severe limitations in adapting to new data environments likely due to the rigidity of their internal representations. Unlike the brains of the London taxi drivers, these deep feedfoward networks cannot inherently self-organize their weight memories to continuously adapt to new environments beyond their training phases.

Self-organization may be able to help with the adaptability of neural networks over time. Similar to self-supervised contrastive techniques, self-organizaiton can support the emergence of clustered latent representations when modeling data distributions without supervised labels. Clusters are often defined by some centroid parameter and this centroid is very similar to codes in codebooks used in quantized networks. Codebooks are a collection of dictionary elements that represent the atomic components, or 'basis' vectors', that the network uses for classification or efficient generation of data using a combination of the codes. In transformer networks, the token vocabulary is essentially a codebook. In other encoders, decoders, and autoencoders, vector-quantized latent spaces implement codebooks as well.

Kohonen Maps

Kohonen Maps are a classical example of self-organizing neural networks within the general class of self-organizing maps (SOM) [12]. Kohonen maps begin as a randomly ordered lattice gradually evolves pushing some cells closer than others resulting in natural cluster formations. The lattice that defines the ordering can reflect spatial 2D topologies or other abstract, multidimensional topological spaces.

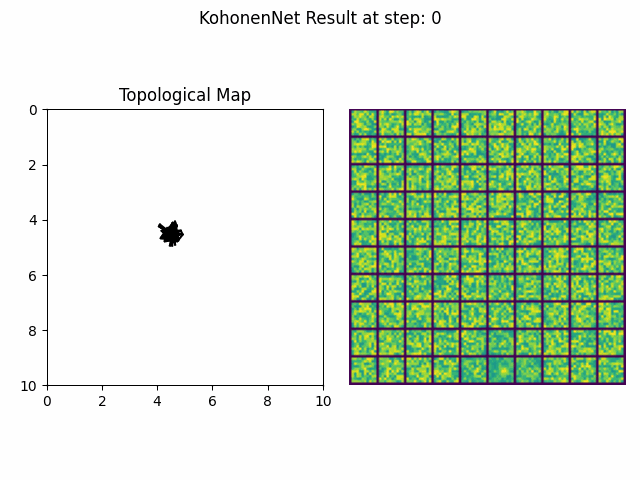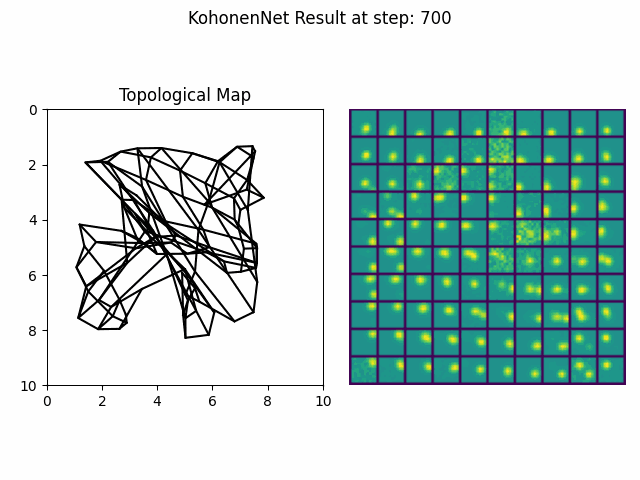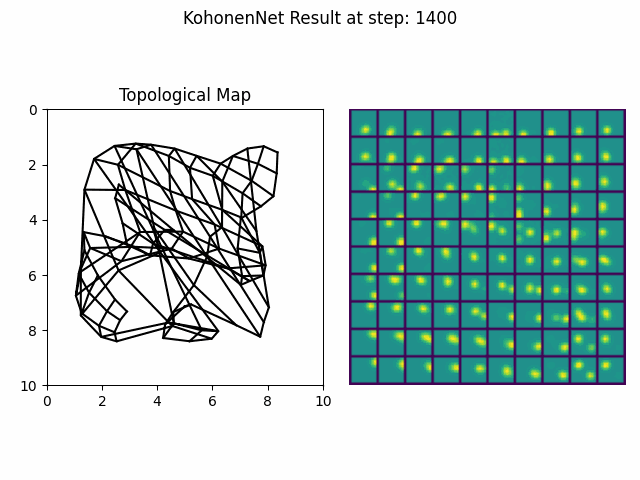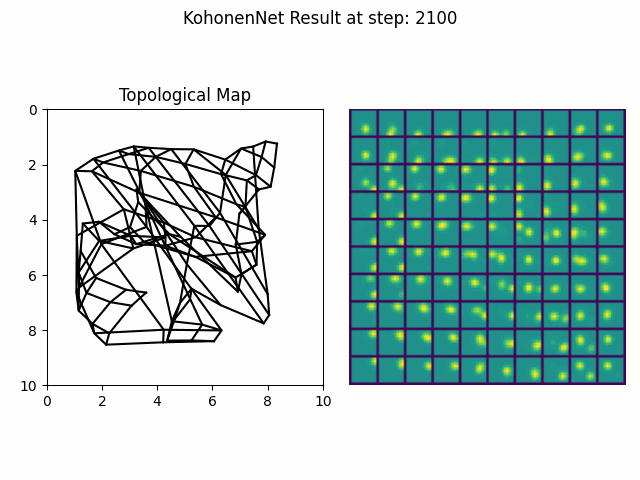Figure 4. An implementation of a self-organizing Kohonen Map in python. It observes images of two-dimensional gaussians appearing in particular configurations and adapts its internal representation over time to best represent the observations.

Sparse coding

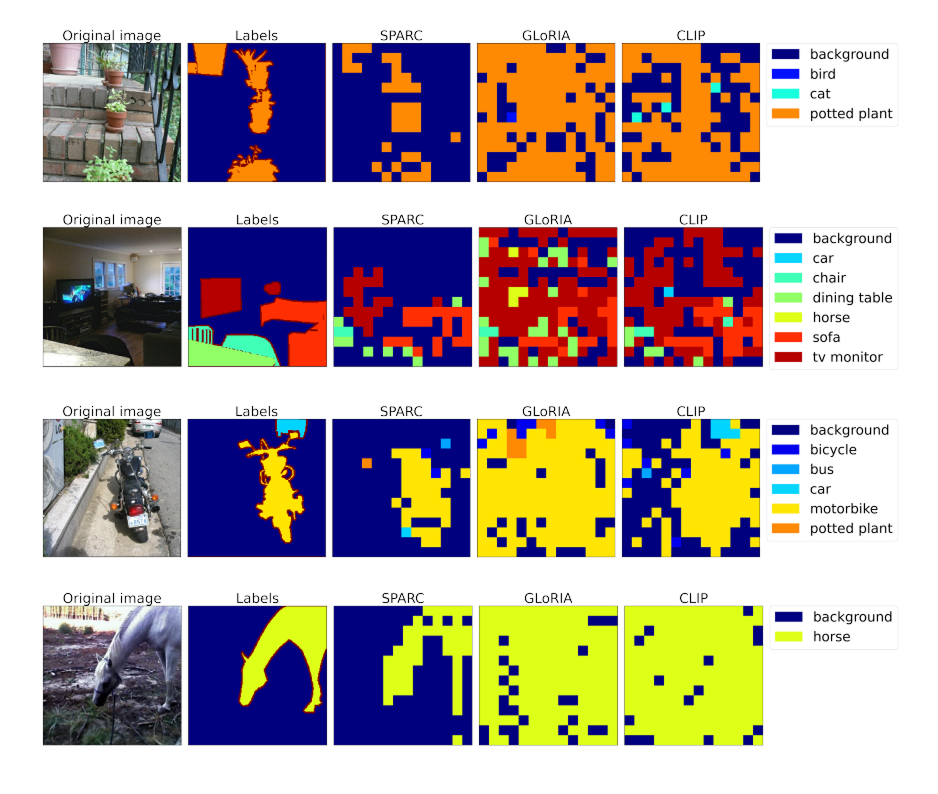
Overcomplete sparse coding can also be interpreted as a self-organizing algorithm because neurons in the network follow local learning rules where they are encouraged to supress the activity of others neurons. A product of sparse coding is a learned dictionary, or code-book, that represents the atomic embeddings of the data. These dictionary codes can then be treated as basis functions in a linear vector space where weighted linear combinations of the data can efficiently recreate the data. Sparse coding can be extended to control pooled groups of neurons (e.g. block-sparsity) or be integrated with additional topological constraints. An interesting result from (Bica et al, 2023) shows how adding sparsity constraints to a CLIP embedding improves fine-grained modeling of text-image pairs [13].

Manifold learning

Manifold learning like SOMs attempts to describe a topology for the embedding space that the model should adhere to during learning. This manifold assumption can be integrated into the objective function for a model as a constraint. Local linear embeddings is one example of manifold learning where the embedding space is assumed to be locally linear, meaning that embedding representations should exhibit a smooth linear interpolation when traversing from one embedding to another.

Future Directions

We explored how generative models can potentially enhance their representational power for multi-modal data distributions by integrating an adapative, online clustering technique via applying self-organizing principles to their learning methods. Modern generative deep networks still do not fully exhibit self-organizing design patterns that leverage local learning rules to modify global structure. Self-organizing elements such as amplification, adapation, cooperation or competition can allow models to have more expressivity and adaptively morph the parameters and structure of the network to reflect changing data environments. Perhaps the general probablistic framework for building this would be like variational expectation maximization for mixture models. This is an exciting research direction that could be extremely rewarding for the field of generative AI with immediate impact on applications such as video generation, robotic vision-langauge-action models, and even agentic systems.

References

• 1. Chebotar et al. "RT-2: Vision-Language-Action Models Transfer Web Knowledge to Robotic Control" arXiv preprint arXiv:2307.15818. 2023


• 2. Stein B., Stanford T., Rowland G. Multisensory Integration and the Society for Neuroscience:Then and Now. Journal of Neuroscience 2 January 2020, 40 (1) 3-11; https://doi.org/10.1523/JNEUROSCI.0737-19.2019.2020


• 3. Sumit Chopra, Raia Hadsell and Yann LeCun. “Learning a similarity metric discriminatively, with application to face verification.” CVPR 2005


• 4. Florian Schroff, Dmitry Kalenichenko and James Philbin. “FaceNet: A Unified Embedding for Face Recognition and Clustering.” CVPR 2015


• 5. Song H., Xiang Y., Jegelka S., Savarese S. "Deep Metric Learning via Lifted Structure Feature Embedding". https://arxiv.org/pdf/1511.06452. 2015


• 6. Kihyuk Sohn et al. “Improved Deep Metric Learning with Multi-class N-pair Loss Objective” NIPS 2016.


• 7. van den Oord, A., Li, Y., Vinyals O. “Representation Learning with Contrastive Predictive Coding” arXiv preprint arXiv:1807.03748 (2018)


• 8. Radford, A., et al. Learning Transferable Visual Models From Natural Language Supervision. 2021


• 9. Caron M., Misra I., Mairal J., Goyal P., Bojanowski P., Joulin A. Unsupervised Learning of Visual Features by Contrasting Cluster Assignments. 2021


• 10. Fini, E., Astolfi, P., Romero-Sorian A., Verbeek J., Drozdal M. "Improved baselines for vision-language pre-training." 2023


• 11. Maguire, E. A.; Gadian, D. G.; Johnsrude, I. S.; Good, C. D.; Ashburner, J.; Frackowiak, R. S. J.; Frith, C. D. "Navigation-related structural change in the hippocampi of taxi drivers". Proceedings of the National Academy of Sciences. 2000


• 12. The Generative Self-Organizing Map. 2003. J.J.Verbeek, N.Vlassis, B.J.A. Kröse


• 13. I. Bica, A. Ilic, M. Bauer, G. Erdogan, M. Bosnjak, C. Kaplanis, A. A. Gritsenko, M. Minderer, C. Blundell, R. Pascanu et al., “Improving fine-grained understanding in image-text pre-training,” arXiv preprint arXiv:2401.09865.2024