Holographic Attention: Part I

Paying attention can get costly

The attention mechanism, a crucial component of transformer-based models, is essential for enabling generative models like ChatGPT to produce coherent and contextually relevant output. This is achieved by learning statistical relationships within sequential data across a large number of samples. However, the attention computation also carries a substantial computational cost, on the order of $O(n^2)$ This high cost makes training and inference for state-of-the-art generative AI models expensive, and also poses challenges for scaling these models economically or deploying them on devices with limited memory.

In this blog series I will introduce a novel theoretical perspective for computing attention based on holographic reduced representation theory. This alternative perspective offers a reformulation of the attention algorithm that can drasactically reduce its computational demands. In this first post I will reveal the aspects of attention that coincide with the holographic representation theory and why holographic representations can be an efficient alternative. Then in subsequent posts, I will explore some recent experiments (including my own) using holographic respresentations to compute attention within transformer neural networks.

Attention Refresher

The development of the attention mechanism emerged largely from the desire to model sequential data in a way that could be parallelized on GPUs [1]. The attention computation essentially re-expresses data samples (i.e. tokens) in terms of the other tokens drawn from the same data sequence. It achieves this re-expression by first leveraging a collection of learned matrix transformations for embedding each of the tokens separately into three different vectors: query, keys, and values. The embedded representations of the keys and queries are then mixed by computing pairwise similarities between each pair of token embeddings. This similarity computation creates a matrix that is of dimension $n\times n$, where $n$ is the number of tokens. Finally, the similarity matrix (a.k.a. attention pattern) is normalized and fed to a softmax operation so all the values along the query dimension integrate to 1 and can therefore be treated as a probability distribution. Token embeddings with higher similarity have values close to 1 and are considered to ‘attend’ to each other.

The $Q{K}^T$ matrix multiplication in this formula makes the attention algorithm’s computational complexity quadratic in space and time. This means that as the input token sequence grows linearly, the memory and compute time requirements for the attention algorithm increases quadractically. This becomes a bottleneck for processing data with large numbers of tokens such as high-resolution images. This constraint is also prohibitive for computing attention on low power, memory efficient, edge devices.

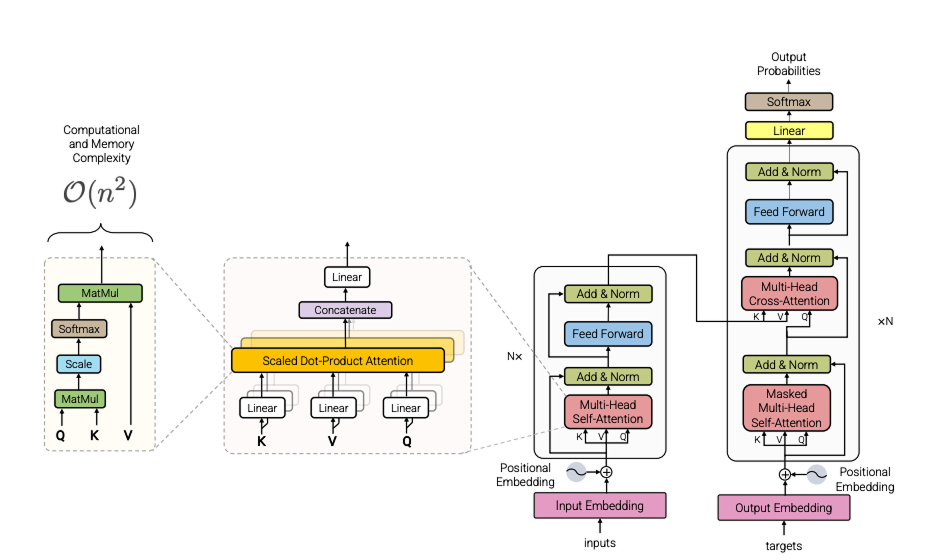
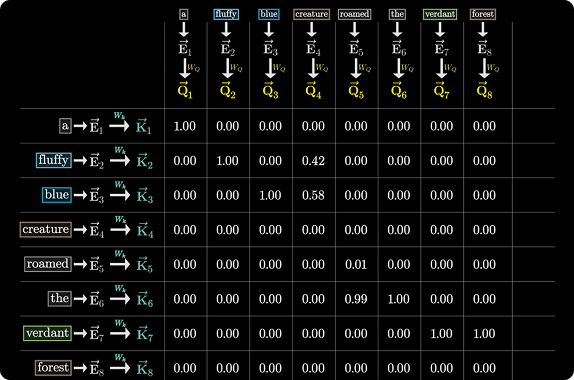Figure 1. Detailed diagram of the full transformer architecture. The scale dot-product attention is the essential building block (Image source: Tay et al [4]) Figure 2. Attention pattern matrix. (Image Source:[3])

More Efficient Attention

Numerous optimizatons have already been explored to reduce the cost of attention both on the software engineering level [3][4] and on the algorithmic level[5]. Efficiency improvements on the algorithmic level would allow transformer models to run cheaper, faster, and on smaller memories universally across all hardware architectures. Most algorithmic reformulations attempt to make linear approximations to attention by exploiting sparse or low-rank structure of the attention pattern matrix. Other methods mix information stored in token embeddings in strategies in novel ways. I'll share just a few of these alternative attention reformulations that will help intuit the holographic approach later on.

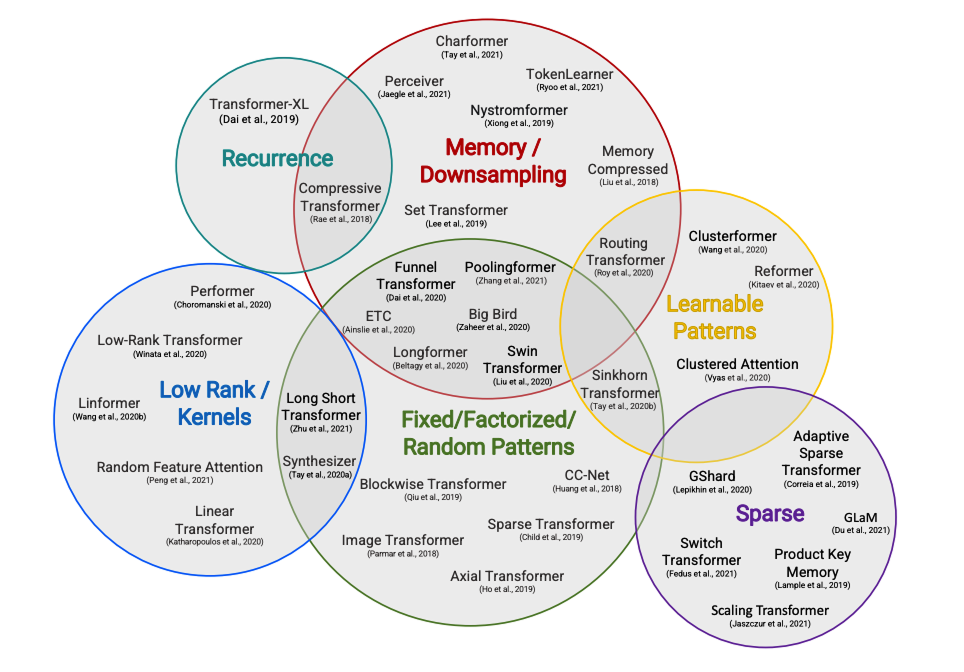Figure 3. Taxonomy of efficient attention methods. (Image source: [4])

Approximations to Attention

One approach to modifying the attention algorithm has been to find low-rank, linear approximations to the attention matrix. This could be straightforwardly done using a SVD decomposition, however the SVD is a prohibitively expensive computation for large matrices. To circumnavigate this, Linformer [8] introduces two linear projections for the key and value matrices to reduce their dimensionality. To further optimize the Linformer, projection layers can share paramenters and different dimensionalities can be used for each layer. Another notable attention approximation is the Performer [7]. The Performer leverages random feature methods[6] with a kernel construction (FAVOR+) to approximate the softmax non-linear function used in attention with low-rank feature maps to achieve linear computational complexity.

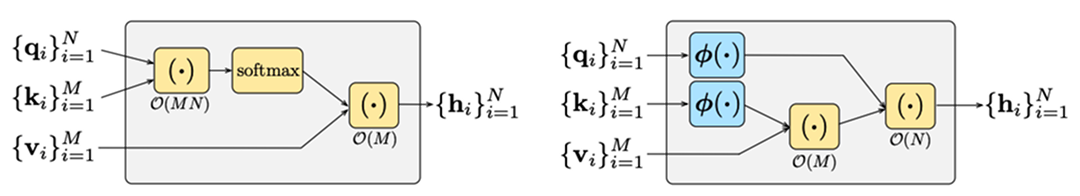
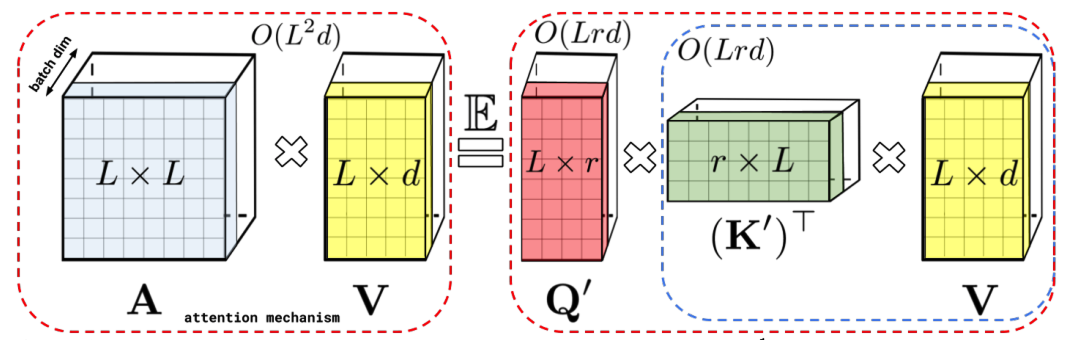Figure 4. (Top) The random feature method computational graph where the softmax is replace by random feature maps(Image Source: [6]). (Bottom) The performer leverages the random feature method to make a low dimensional approximation of AV. (Image Source: [7])

Information Mixing for Attention

Another alternative to computing attention considers new ways to “mix” information stored in the token embeddings. The MLP Mixer[9] approach mixes features across spatial locations and signal channels in images through two multi-layer perceptron layers, precluding the need for attention or convolution. FNet[X] utilizes the fourier transform to mix information across tokens replacing the attention computation altogether and achieving up to 97% of the accuracy of transformer-based model counterparts on the GLUE benchmark while training 80% faster on GPUs. FFTNet extends the FNet approach to enable learning of adaptive spectral filters to efficiently model long-range dependencies. One other method worth mentioning is the Reformer. Although not often classified as a mixing approach in literature, I believe it shares some of the same logic. The Reformer solves the problem of finding nearest neighbors quickly in the high dimensional embedding space using locality-sensitive hashing. This hashing scheme preserves information distances reflecting the similarity of embeddings, thus information is effectively mixed through clustering. Both fourier mixing and the Reformer achieve $O(n\log n)$ complexity.

Holographic What?

First, it’s important to build some intuition about holographic representations. For brevity, I will only disucss parts of the theory that are important to understanding to the topic of computing attention. However there is a growing body of great papers and resources online. In particular, I highly recommend this site (link) which was developed from my graduate lab, The Redwood Center for Theoretical Neuroscience (link) , where some of the lead vector symbolic architecture researchers work.

Holographic Reduced Representations (HRR) is a thread of symbolic AI research that has been explored since the 1990s, with the earliest work put forth from researchers such as Tony Plate and Penti Kanerva. Today the field has more or less converged on Vector Symbolic Algebras or Vector Symbolic Architectures (VSA) as the overarching name for this general class of symbolic computing frameworks of which HRR is a subset. What I will explore in this and subsequent articles need may be generalized to other VSA variants, but HRR will anchor us with concrete algorithmic implementations and intuitions that carry over from some of the attention methods mentioned earlier.

It's imporant to note that symbolic AI has some different perspectives on building intelligent systems compared to modern deep learning. For example, deep learning emphasizes the construction of some objective function and applying a differentiable computational graph (deep neural net) to transform data from some input to a desired output in service of that objective function. Understanding the data representations that emerge within the middle of the large neural networks is somewhat of a after-thought for deep learning. Symbolic AI, broadly speaking, places more emphasis on building efficient, adaptable, and interpretable representations of data from the outset. Learning and reasoning then typically manifests as operations and manipulations on these symbolic representations. While HRR shares this alternative, symbolic computing principle, it is common in contemporary research to leverage deep neteworks for some stages in VSA-based algorithms. Thus, HRR can encompass deep learning and deep learning can utilize HRR modules in neural networks, the latter of which we will see for our exploration of holographic attention.

Figure 5. Example of a symbolic approach to reasoning using vector symbolic algebra. (Image Source: [12])

Okay, so what are these mysterious holographic representations? They are essentially high-dimensional vector (hypervector) representations (10,000+ in dimension). The motivation for the hypervector representations is rooted in the statistical nature of randomness in high-dimensional spaces. In high dimensional spaces (~10,000 dimensions or larger), all random vectors are nearly orthogonal which can be hard to intuit. This insight is important to the theory because it enables data mapped to this space to automatically enjoy an uncorrelatation with respect to its neighboring samples. If that doesn't make sense right away, we can think of the fourier transform as an analogy. When a fourier transormation is applied to a signal, the signal is broken down into a linear combination of many sinusoidal functions. All of the fourier components (harmonics) are naturally orthogonal to each other and thus uncorrelated with each other (dot product is zero). For holographic representations you can think of each random hypervector as a fourier component which are (mostly) orthogonal to other hypervectors. The exact implementation of the hypervectors has been done in many different ways. Research as explored binary, bipolar, continuous real, and continous complex hypervectors. Techinically holographic reduced representations (HRR) refer to the class of models that use continuous real valued hypervectors.

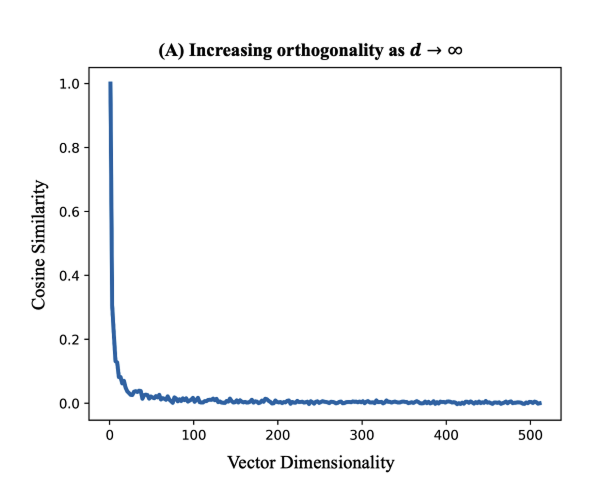Figure 6. Statistical structure of holographic reduced representations. It is visible here in a low-dimensional projection that similar random vectors exhibit a peaked distribution with rapid fall off.

Once we have the holographic representation vectors, the theory presents just three primitive operations that can be applied to the hypervectors : Binding, Superposition, and Permutation.

Binding/Unbinding

The binding operation combines hypervectors to produce another hypervector that has the same dimension of the input hypervectors. The resulting hypervector is dissimilar to the input hypervectors, thus binding can be interpreted as a randomizing operation that moves the compound representation of the input hypervectors to another (random) part of the the high dimensional space.

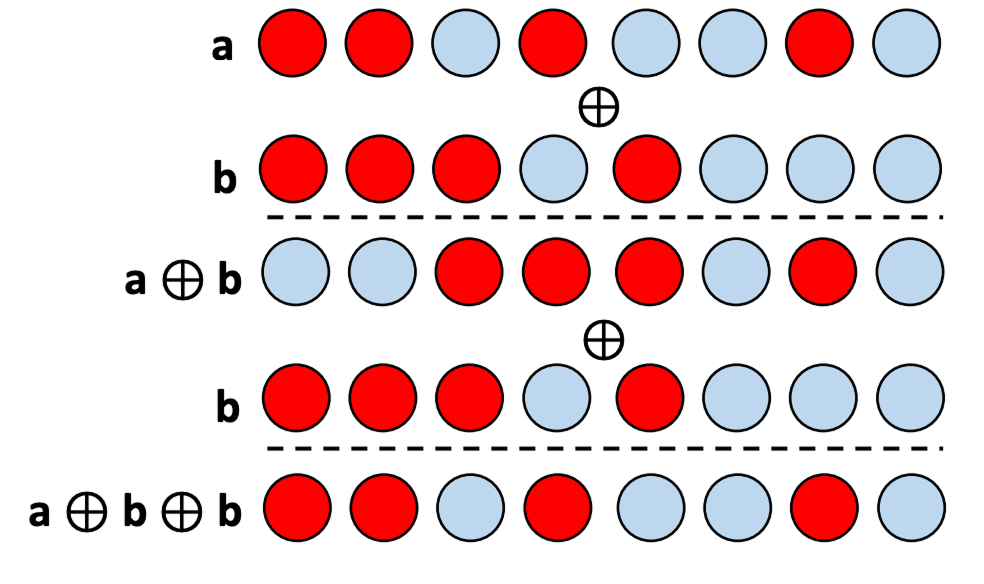
Figure 7. Binding operation on binary vectors using an XOR operation represented with $\oplus$ .(Image Source:[])

The binding operation is also reversible in that the resulting hypervector can be decomposed back into either of the input hypervectors with the inverse operation, unbinding. The unbinding operation is applied between one of the input hypervectors and the bound hypervector and the output would be the other input hypervector. In practice, this operation is not perfect especially when there are many hypervectors sharing the same embedding space. Thus the unbinding operation typically results in an output that includes noise that must be removed. For holographic hypervectors, the binding and unbinding operation are both implemnted with circular convolution, while other models may use other methods such as the hadamard products or XOR operations on binary vectors for example.

Figure 8. Binding operation represented as circular convolution operation (Image Source:[13])

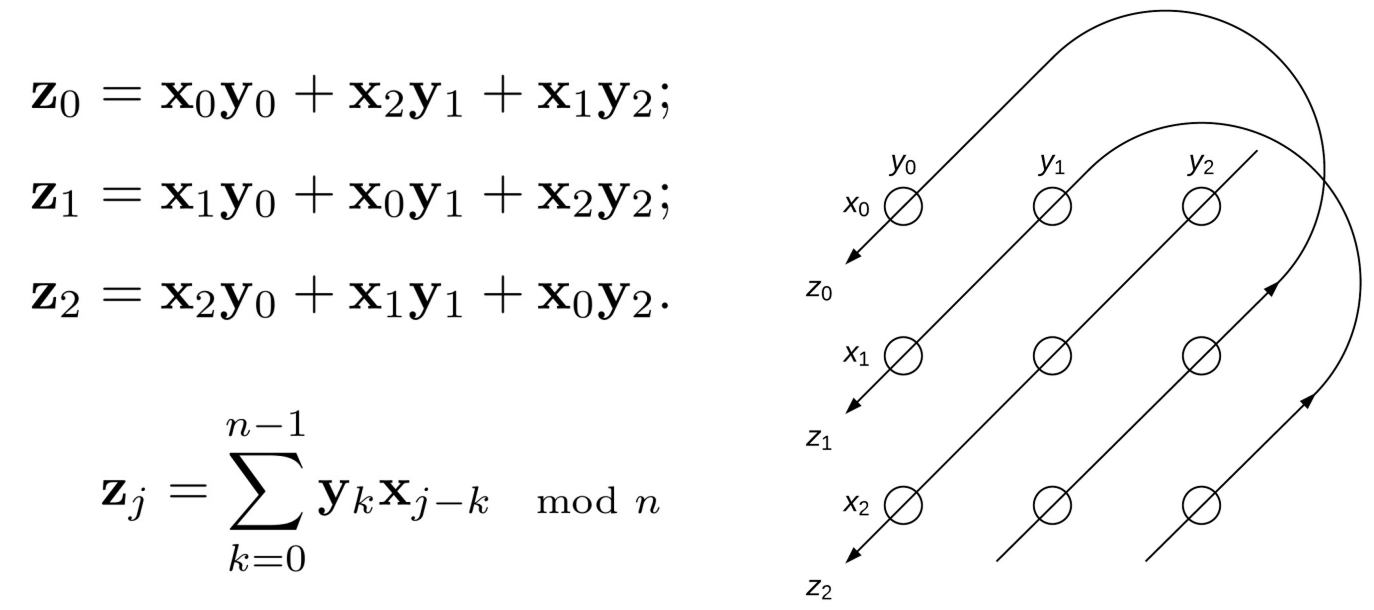
Superposition

Superposition is an operation that can combine hypervectors in a way that also preserves the dimension of the original vectors but unlike binding, it creates a new hypervector that shares similarity with the input hypervectors.

Permutation

The permutation operation is unitary and primarily used to represent sequential ordering of a sequence of symbols. An example of a permutation operation for a hypervector would be to rotate the all of the index valuee to the neighboring index. The output of a permutation operation is a hypervector that is dissimilar to its input, similar to the binding operation.

So, how does one get to these holographic representations? Well, VSA doesn't specify any one prescription for arriving at those representations. The representations are embeddings of observed data, so one approach is to use efficient encoding methods to learn high-dimensional embeddings with autoencoder-type networks. One can also just sample random projections in high dimensions for each data sample.

In summary, holographic representatons are are high-dimensional and highly distributed representations and can be manipulated with a small set of symbolic operations. The main ideas to take thus far for understanding hologoraphic representations are: in high dimensions, most random vectors (hypervectors) are orthogonal and composing with the hypervectors with the three primitive operations can be used to build representations in a compositional and reversible way. The reversibility will play a key part in the utility and some of the challenges in using this approach. A helpful mneumonic for computer science-minded folks is that holographic representations is like a high dimensional content-addressable memory system (e.g. vector database) with some simple, compositional operations.

Towards Holographic Attention

So where and how does holographic representations intersect with computing attention? The intersection can be seen from multiple directions. This is a very new research direction, thus there are likely to be more interpretations that have yet to be fully articulated.

The framing of the original attention in terms of keys, queries, and values relates strong relation to databases. Attention can thus be considered as a type of content-addressable associative memory or fuzzy database. One special characteristic about the attention mechanism, is that the neighboring data influencing the new representation need not be confined to a local window, as with convolutional methods, but rather the neighboring data can be near or far (in space or time). Once all the data is processed, the internal network representations formed from attention layers basically distribute the information contained in a single token embedding to all the other token embeddings. The construction of embeddings that combine information from many different data chunks can be seen as a form of distributed memory, where the information about one particular data chunk(token) is distributed amongst the others.

Another way that holographic representation theory can be seen to intersect with attention is from the perspective of information mixing. The formation and evolution of the attention matrix can be framed as mixing as presented earlier in the the description of efficient attention methods. As the attention matrix evolves during training, information contained in one token is routed more to some selective tokens than others. In hologrpahic representations, the binding and superposition in essence conduct a mixing of information while also being able to reversibly factor individual components that form a mixture. Fourier mixing strategies are perhaps some of the closest methods mechanistically to the holographic representation approach given their use of the fourier transform.

To be continued...

Great, if you made it this far you are a trooper! Hopefully I was able to shed some light on how holographic representation theory can be relevant in computing attention for neural networks. In the subsequent blogs for this series, I will share concrete implementations integrating holographic representations and operations for the attention computation in transformer networks.

References

• 1. Ashish Vaswani, et al. “Attention is all you need.” NIPS 2017.


• 2. Sanderson G. "Visualizing Attention, a Transformers Heart"https://www.3blue1brown.com/lessons/attention. 2024


• 3. T. Dao, D. Fu, S. Ermon, A. Rudra, and C. Re, “Flashattention: ´ Fast and memory-efficient exact attention with io-awareness,” Advances in Neural Information Processing Systems, vol. 35, pp. 16 344–16 359. 2022


• 4. Kwon W., Li Z., Zhuang S., Sheng Y., Zheng L., Yu C., Gonzalez J., Zhang H., Stoica I. "Efficient Memory Management for Large Language Model Serving with PagedAttention"https://arxiv.org/abs/2309.06180. 2023


• 5. Peng et al. “Random Feature Attention.” ICLR 2021.


• 6. Choromanski et al. “Rethinking Attention with Performers.” ICLR 2021.


• 7. Tang Y., Dehghani M., Bahri D., Metzler D. "Efficient Transformers: A Survey" arXiv preprint arxiv.org/pdf/2009.06732 (2022).


• 8. Wang et al. “Linformer: Self-Attention with Linear Complexity.” arXiv preprint arXiv:2006.04768 (2020).


• 9. Tolstikhin I. et al. "MLP-Mixer: An all-MLP Architecture for Vision". arXiv preprent arxiv.org/pdf/2105.01601 (2021).


• 10. Lee-Thorp J., Ainslie J., Eckstein I., Ontanon S. "FNet: Mixing Tokens with Fourier Transforms" Proceedings of the 2022 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies doi: 10.18653/v1/2022.naacl-main.319


• 11. Fein-Ashley J., Kannan R., Prasanna V. "The FFT Strikes Again: An Efficient Alternative to Self-Attention" arxiv preprint arxiv.org/pdf/2502.18394 (2025)


• 12. Kanerva, P. "What We Mean When We Say 'What's the Dollar of Mexico?': Prototypes and Mapping in Concept Space" AAAI Fall Symposium Series (2010)


• 13. Plate, T. "Holographic Reduced Representations" IEEE Transactions on Neural Networks Vol. 6, No. 3 (1995)


• 14. Osipov E., Kahawala S., Haputhanthri D., Kempitiya T., De Silva D., Alahakoon D., Kleyko D. "Hyperseed Unuspervized Learning with Vector Symbolic Architectures" IEEE Transactions on Neural Networks Vol. 35, No. 5 pp. 6583-6597, May 2024, doi: 10.1109/TNNLS.2022.3211274 (2022)