January 23, 2020

Unsupervised Video Encoding

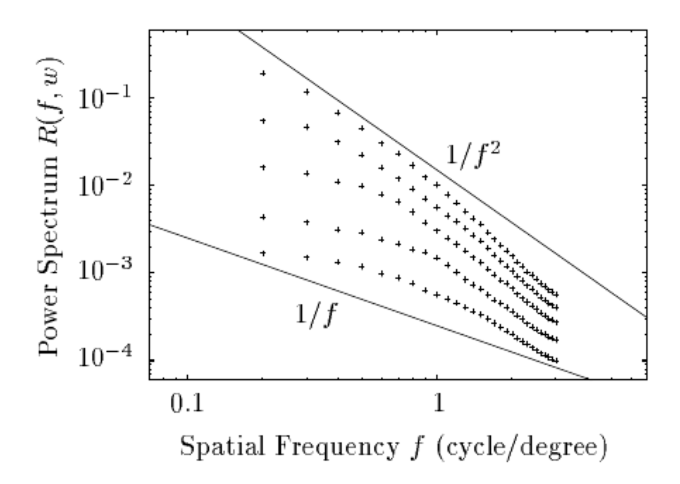
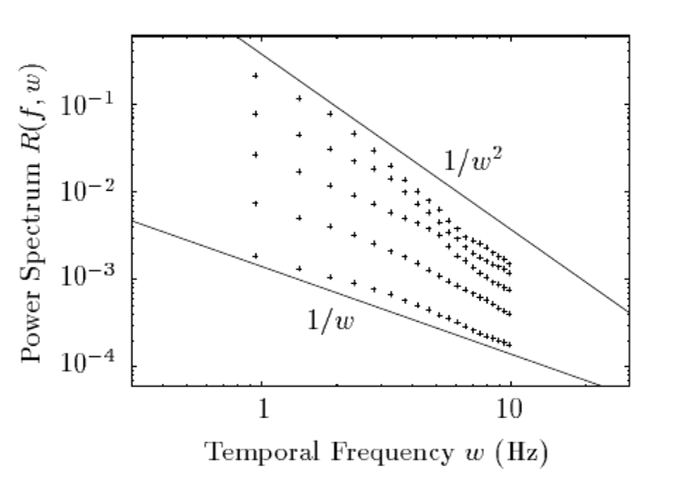
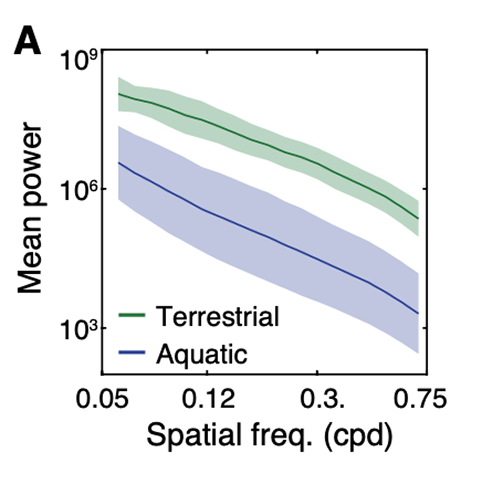
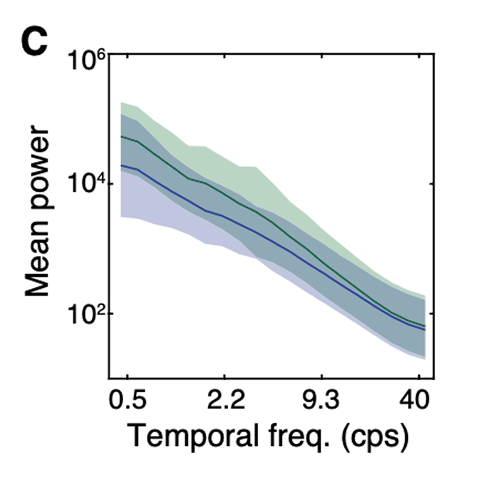
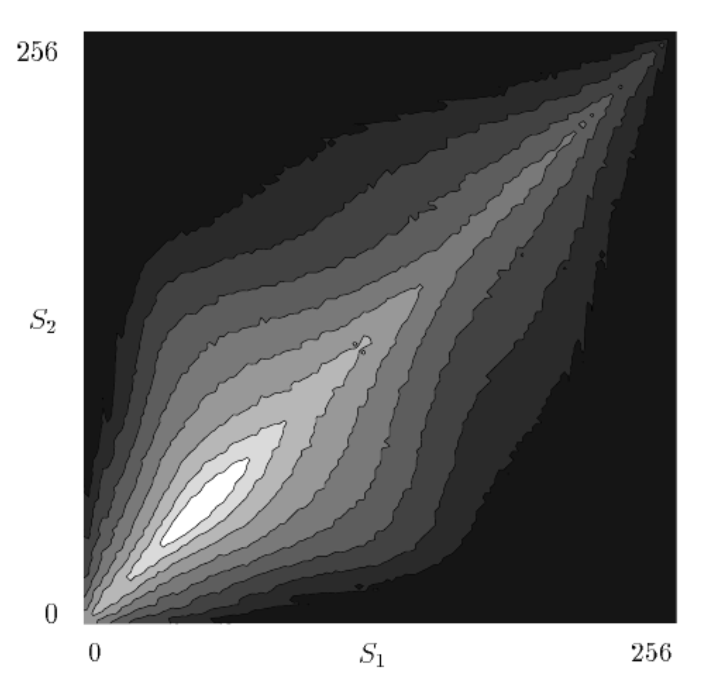
Natural video scene statistics

The brain is an inference machine, yet universal computational algorithms supporting this inference remain largely unknown. The efficient coding hypothesis suggests that the brain extracts statistical structure from noisy sensory data to construct a coherent model of the natural world [1][2]. Research has demonstrated that natural visual scenes have distinct spatiotempal statistical structure at several different scales [2][3]. Here we explore a bio-inspired generative model that uses sparse coding to learn this spatiotemporal structure in natural video scenes.

Figure 1. Spatial and temporal frequency statistics of natural scenes. (Left) Seminal research from Dong & Atick revealing the power-law distribution relationship between signal intensity and signal frequency in spatial and temporal domains. (Image Source: [1]) (Right) Recent research from Cai, Cooper et al [2] has also found this statistical relationship to exist similarly in aquatic and terrestrial environments. (Image Source: [2])

Figure 2. Measured pairwise probability distribution for two similar spatial locations separated by 33 ms in time. White (black) represents high (low) probability. This illustrates high correlation between the two light intensities within small separations of time, suggesting a general spatio-temporal statistical structure for natural moving scenes(Image Source: [1])

Sparse coding with LCA

Sparse coding is a well-explored method for unsupervised learning of statistical structure in data especially in high dimensional spaces. Unlike typical compression or bottle-neck autoencoders which simply map high-dimensional data to low dimensional spaces, sparse coding instead maps high-dimensional data to an overcomplete, higher dimensional embedding space but constrains the active components representing a single signal to a low dimension. The theory posits that efficient representations are formed under resource constraints and thus latent variables undergo competition to create encodings that are maximally expressive with the minimal active (non-zero) variables. The higher dimensional representational space adds fidelity, expressivity, and robustness to the encoded information as each representation becomes nearly orthogonal to the others (maximally uncorrelated). Image data is a notoriously high dimensional domain where sparse coding has also been applied extensively. Remarkably, it was shown in Olshausen et al. [4] that when applied to natural images, sparse coding learned latent representations that matched the tuning properties of simple cells in the V1 area of the primate visual cortex. When visualized in the image domain, these representations resemble "edge-dectors" or wavelet filters. Importantly, unlike hand-engineered wavelet filters, sparse coding's representation are learned from data in an unsupervised manner based on a generative model.

Sparse coding can be modeled as a linear generative equation as the following:

$s = a Φ + v$

The additional term $v$ represents the noise in the model which is assumed to be $∽ N (0, Σ)$ , drawn from a Gaussian with 0 mean and diagonal variance $Σ$ .
The objective function for denoising the input with a sparsity constraint is the following:

$\underset{a}{argmin} (E_{s c} = \frac{1}{2} ∥ s - Φ ∥ + (λ \sum_{k = 1} C (a_{k})))$

Sparse coding can be implemented as an autoencoder with shared encoder-decoder weights or as a single-layer recurrent neural network with all-to-all connections, like a Hopfield network. Sparse coding models are typically trained to denoise and compress data. Signals are fed to the network which then under goes an interative winner-takes-all greedy algorithm to select the most useful feature vectors to reconstruct the signal.

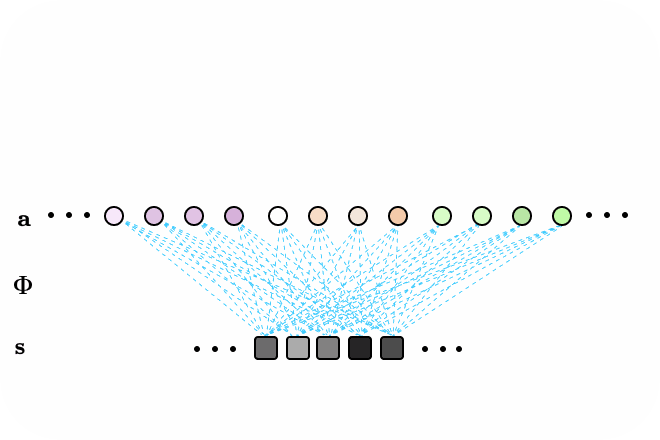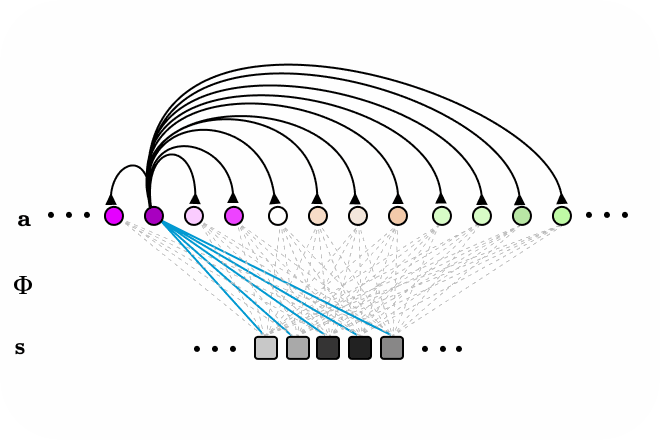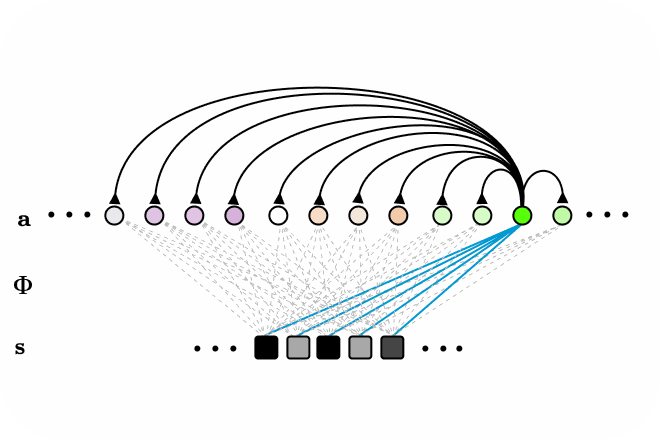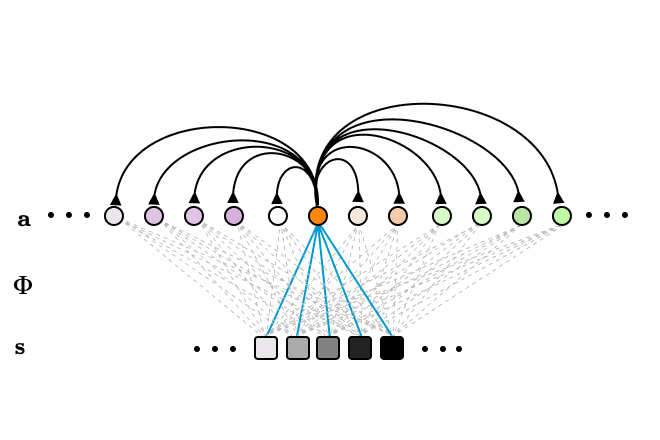Figure 3. LCA animated as a recurrent neural network, with all-to-all connections. Neurons surpassing the activation threshold, supress the activity of all other neurons, encouraging a sparse encoding. Connections between neurons omitted for clarity.

LCA is a class of neural networks that implement sparse coding effciently as a dynamical system, taking inspiration from leaky-integrate and fire models of biological neurons which have internal states and external activations. Neurons integrate their internal state value, until an activation threshold is surpassed, increasing the value of the external state variable a. Active neurons supress the activity of all other neurons, encouraging a sparse encoding. These models are neat, because they can also be implemented in low power analog circuits.

The internal state of neurons over time for LCA can be modeled as a nonlinear ordinary differential equaiton (ODE) with the following dynamical equation:

$\dot{u_{m}} (t) = \frac{1}{τ} [b_{m} (t) - u_{m} (t) - \sum_{k \neq m} G_{m, n} (a_{n} (t))]$

The full dynamic system equationn for LCA can then be written as:

$\hat{s} (t)$

where

$a (t) = T_{λ} (u (t))$

This ODE, has an equivalent mathematical expression as the continuous Hopfield Network model.

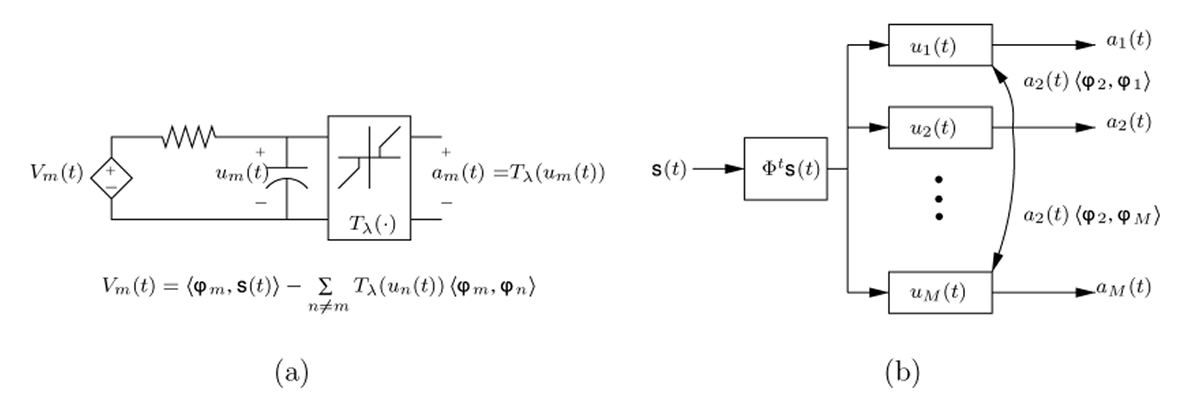Figure 4. The original locally competitive algorithm (LCA) represented as an analog circuit. Where u represents the internal state of the neurons and a represenst the external state. Connections between neurons omitted for clarity. (Image source:[5])

Subspace LCA

In our study, we extend the LCA to investigate efficient encoding of natural video. We augment LCA into a heirarchical, two-layer model. The second layer design was inspired by latent variable models, factorized representations, and disentanglement theories of perception. We hypothesized that first layer neuron representations could be further composed into a representation that disentangled motion from form via a second layer computation. The second layer neurons could be then potentially learn an efficient, higher order statistic of the data based on the subspaces formed by the features learned in the first layer.

The second layer neurons group the responses of the first layer neurons, introducing an aspect of locality. Instead of all first layers neurons having equal influence on other first layer neurons, groups of neurons can now only co-influence their second layer neuron to become active. The second layer neurons, however, can influence any other second layer neurons. This result of this design shares some similarity to block-sparse coding whereby groups of cells are turned on or turned off together at the same time. The activation values of the second layer neurons are determined by the energy of within group first layer neuron activities. Here we chose the L2 norm, although there are many other possibilities that could be interesting to explore.

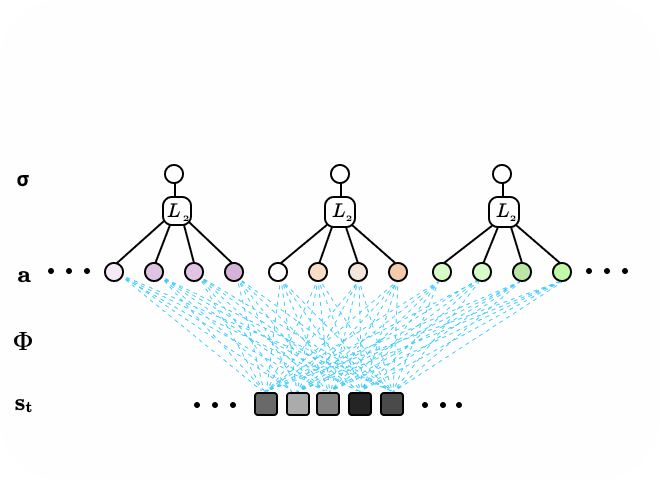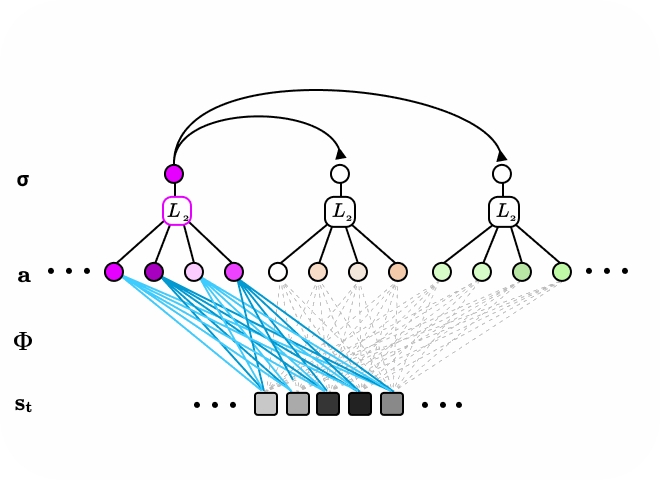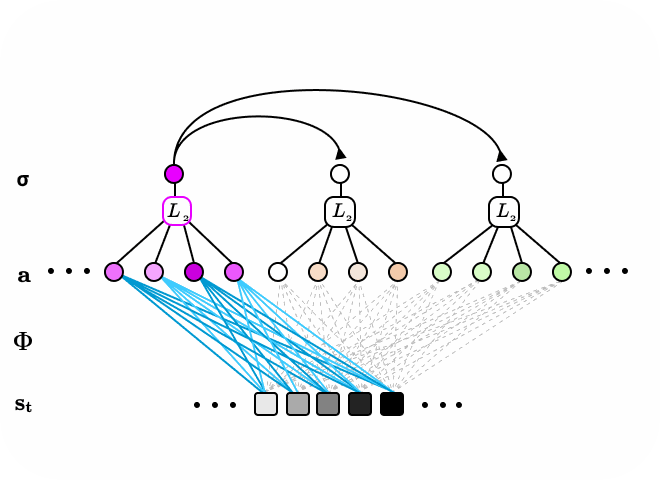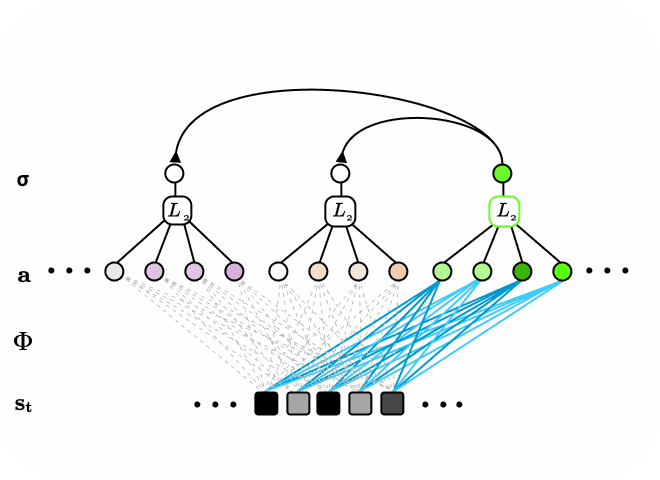Figure 5. The subspace locally competitive algorithm (SLCA) illustrated as two-layer recurrent neural network. Latent nodes in first layer have all-to-all,reccurent, lateral connections. Additionally, a second layer of neurons form subspaces over the first layer via pooling first layer responses. When input data is sequential or time-varying, the network is encouraged to learn different representations in the first and second layers.

We consider the pooling second layer as subspaces spanned by basis vectors learned in the first layer. One could also interpret Subspace LCA (SLCA) as introducing a topological ordering constraint on the first layer neurons in LCA via a neighborhood, pooling function. The topological ordering here refers to one that is more general than the x-y spatial domain of the data input, and instead refers to the topology of an abstracted feature space of high dimensions.

The training objective for the network was to reconstruct time-varying, natural video data. The new SLCA objective function can be expressed as the following:

$\underset{a}{argmin} (E_{s l c a} = \frac{1}{2} ∥ s - \sum_{i = 1} \sum_{j = 1} σ_{j} z_{i j} Φ_{i j} ∥ +$ $λ \sum_{j = 1}^{N} σ_{j} + β \sum_{i = 1}^{N} \sum_{j = 1}^{M} \sum_{l = 1}^{M} Φ_{i} Φ_{i} - I_{N})$

Our dataset was sourced from the Hyvarinen video dataset of natural scenes (e.g. ducks in a pond or birds in a tree) and head-mounted camera footage from a student walking on UC Berkeley college campus. We extracted 16x16 patches of each frame across various time lengths in the video to train and evaluate the network.

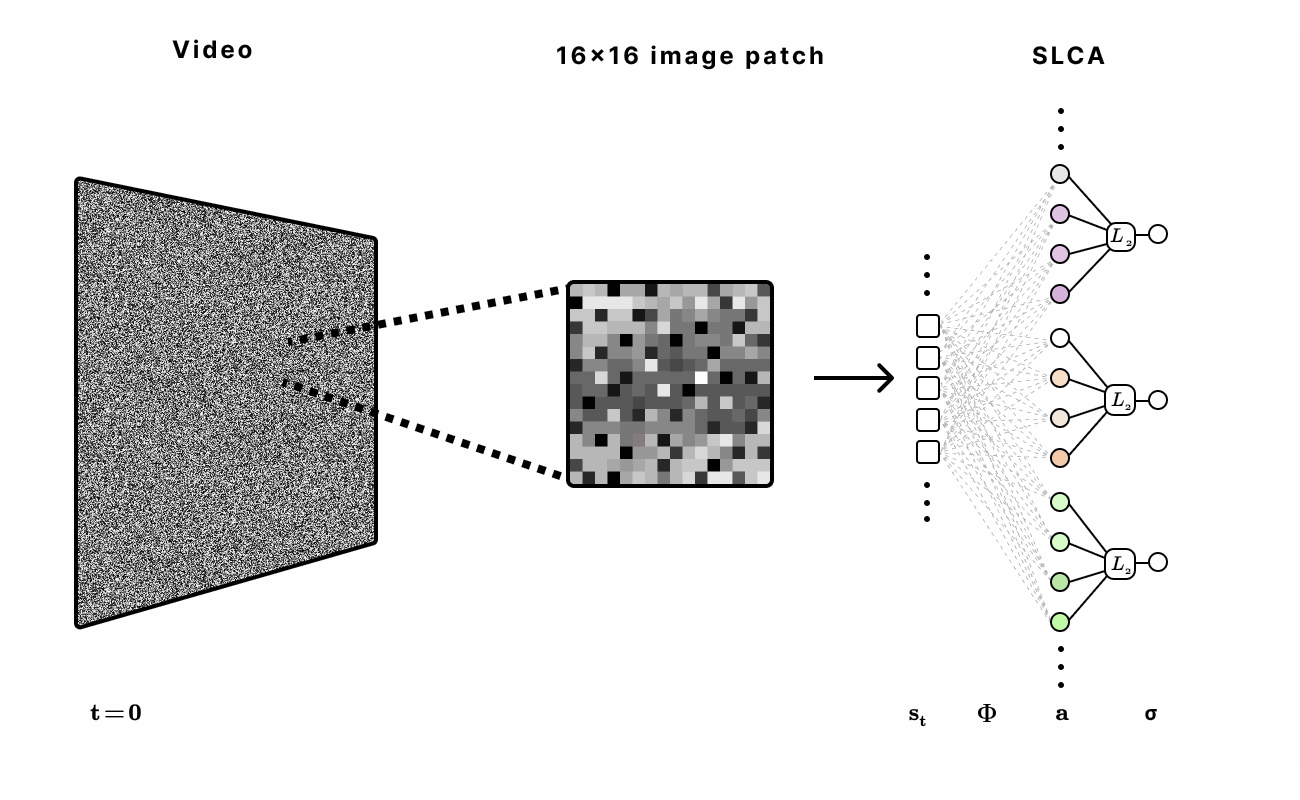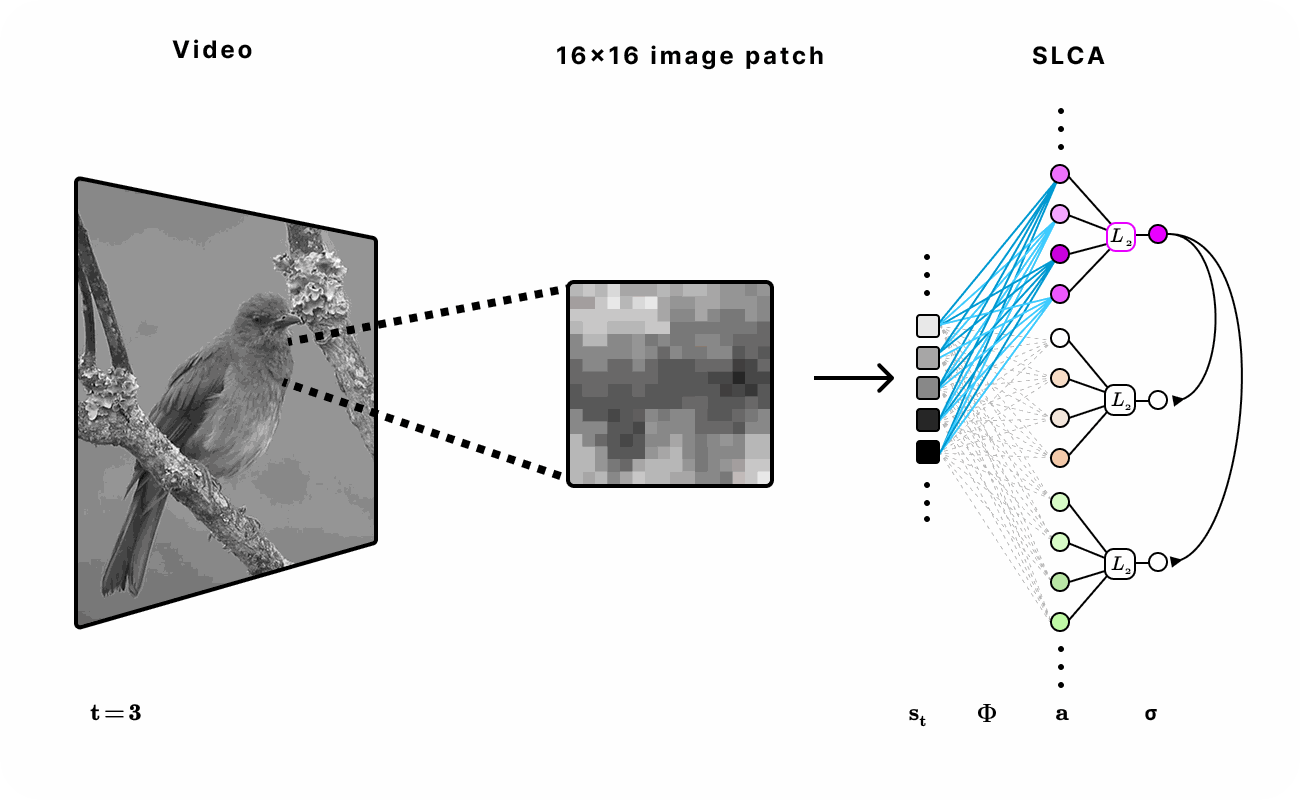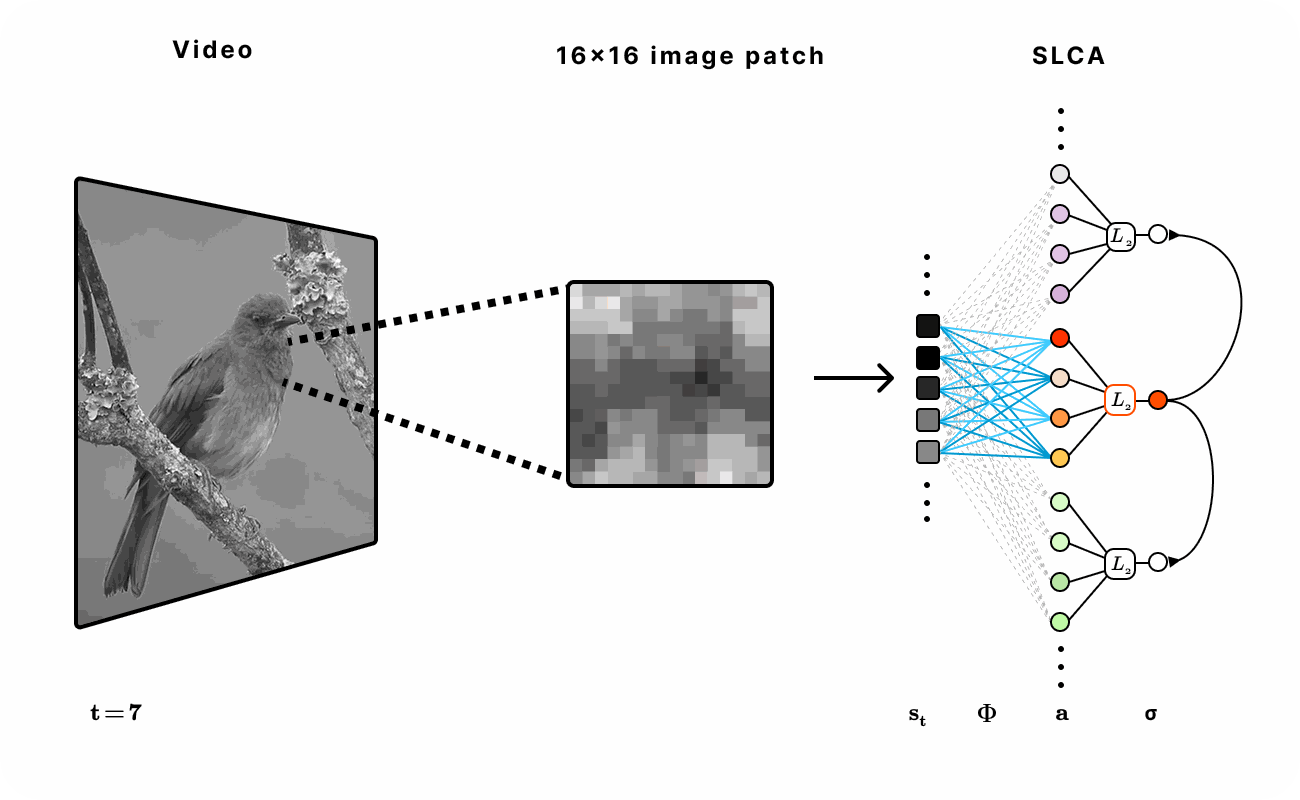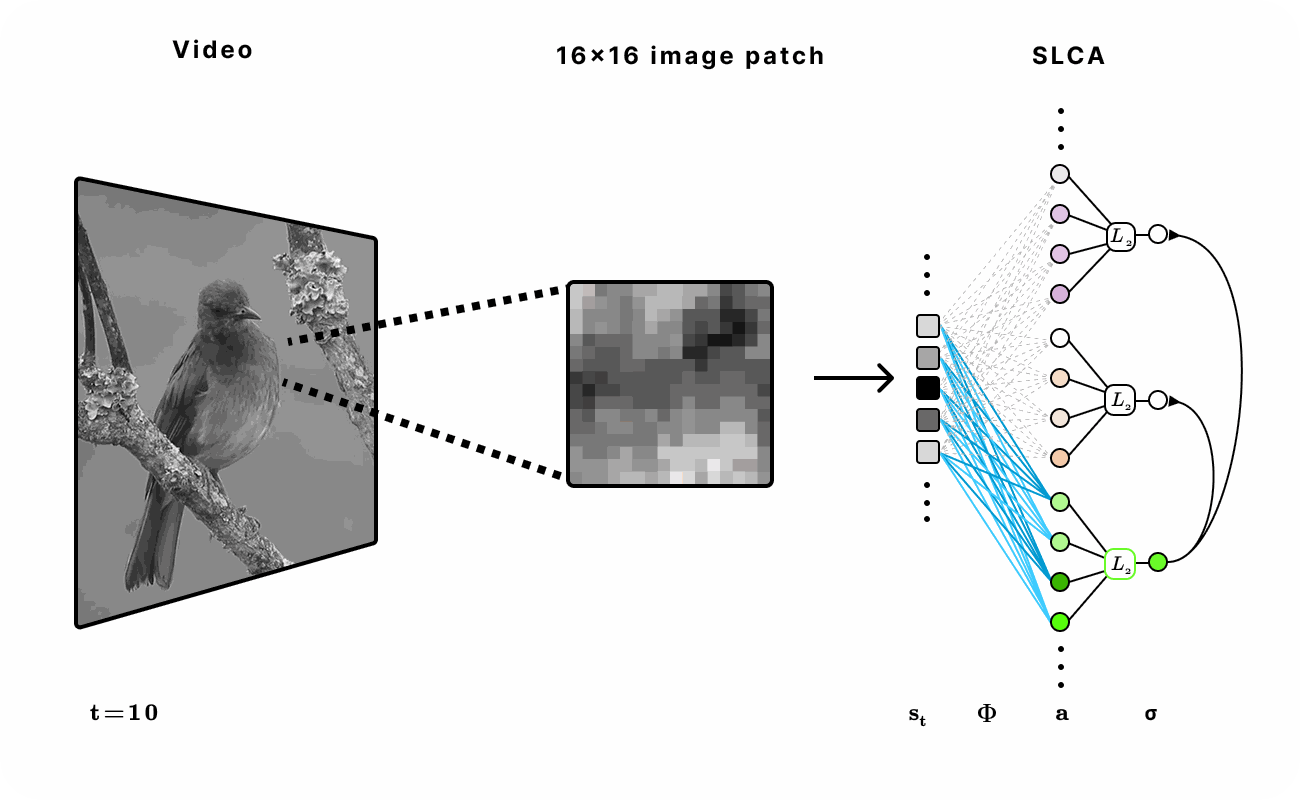Figure 6. Experimental setup for encoding natural video with SLCA. 16 x 16 patches were first extracted from the video and then fed into the recurrent SLCA network. The dimensionality of the latent representation was varied from 1x to 5x of the input dimension.

Results

Figure 7. Visualized learned features grouped by subspace. The subspaces appear to learn to span some transformations space on a feature vector which allows the second layer neuron activations to be invariant to those within-group transformations.

After applying the subspace topological constraint on the SLCA model, we discovered interesting insights into the characteristics of the learned latent features and their subspaces. We found that the first layer learned “edge detector”-like features similar to previous research [1], while the second layer neurons learned to group first layer features that shared general shape and orientation but varied in phase and spatial translations (Fig 3). These results suggest that the learned subspaces can be invariant to spatial translations and phase modulations in the observed data. These translations and modulations correspond to motion in visual perception [6]

The temporal behavior of the second layer neurons compared to the first is also revealing. For video, these second layer neurons activations were also more stable over time compared to the first layer, suggesting an adherence to a manifold.

Figure 8. Temporal stability appears stronger for second layer neurons compared to first layer neurons.

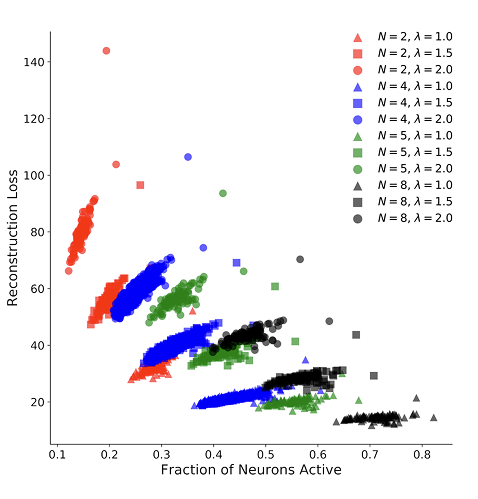Figure 9. Visualized learned features grouped by subspace. The subspaces appear to learn to span some transformations space on a feature vector which allows the second layer neuron activations to be invariant to those within-group transformations.

Conclusion

There are several interesting takeways from this experiment for unsupervised encoding of video in a overcomplete sparse coding network. First, heiarachical structure appears to be necessary to express the high-order dependencies intrinsic in video. Additionally, the higher-order statistical structure can be extracted with topological grouping introduced in a layer beyond the first layer of processing. Data reconstruction also appears to be benefitted by increasing the number of first-layer units within a group. However, as the group size grows, there will also be a growth in the fraction of neurons that will need to be active to maintain a low reconstruction loss. Our experiments show that a good efficiency trade-off occurs arround group sizes of four where roughly a third of the neurons within the group are active. Future interesting research directions could explore scaling this network to process larger frames and on full color video.

References

1. Dong, D. W. & Atick, J. J. Statistics of natural time-varying images. Netw. Comput. Neural Syst. 6(3), 345–358 (1995).

2. Cai L., Krishna V., Hladnik T., Guilbeault N., Vijayakumar C., Arunachalam M., Junti S., Arrenberg A., Thiele T., Cooper E. Spatiotemporal visual statistics of quatic environments in the natural habitates of zerbrafish. 2023. doi: 10.1038/s41598-023-36099-z.

3. van Hateren, J. H. A theory of maximizing sensory information. Biol. Cybern. 68(1), 23–29 (1992).

4. Olshausen BA, Field DJ. Sparse coding with an overcomplete basis set: a strategy employed by V1? Vision Res. 1997 Dec;37(23):3311-25. doi: 10.1016/s0042-6989(97)00169-7. PMID: 9425546.

5. Rozell C., Johnson D., Baraniuk R., Olshausen B. 2008 Sparse Coding via Thresholding and Local Competition in Neural Circuits.

6. Cadieu C., Olshausen B. 2011 Learning Intermediate-Level Representations of Form and Motion from Natural Movies

Self-organizing multimodal codes

Aug 29, 2023

Holographic Attention: Part I

Apr 23, 2022